공분산,상관계수,span,basis,rank_Day12(3)

[지난주 복습]

Variance (분산)

분산은 데이터가 얼마나 퍼져있는지 측정하는 방법

 

모집단의 분산 σ2 는 모집단의 PARAMETER (aspect, property, attribute, etc)이며,

샘플의 분산 s2 는 샘플의 STATISTIC (estimated attribute)입니다.

샘플 분산 s2 는 모집단 분산 σ2의 추정치

 

Standard Deviation (표준편차)

표준편차는 분산의 값에 (√)를 씌운 것

---

• Covariance (공분산)

1개의 변수 값이 변화할 때 다른 변수가 어떠한 연관성을 나타내며 변하는지를 측정하는 것

 

 

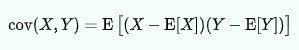
• Correlation coefficent (상관계수)

분산에서 스케일을 조정하기 위해 표준편차를 사용했던 것처럼,

공분산의 스케일을 조정하는 방법.

공분산을 두 변수의 표준편차로 각각 나눠주면 스케일을 조정할 수 있으며 이를 상관계수라고 부른다.

상관계수는 -1에서 1까지로 정해진 범위 안의 값만을 갖으며 선형연관성이 없는 경우 0에 근접

 

• * 추가 *

Spearman correlation (데이터가 categorical 일때 사용할수있는 상관계수 계산법)

correlation coefficent ( = Pearson correlation , 데이터가 numeric 일때 사용할수있는 상관계수 계산법)

 

 

• Orthogonality (수직)

벡터 혹은 매트릭스가 서로 수직으로 있는 상태

(임의의 두 벡터의 내적값이 0인지를 통해 파악)

 

 

• 단위벡터 (Unit Vectors)

단위 길이 (1)을 갖는 모든 벡터

 

• Span

주어진 두 벡터의 (합이나 차와 같은) 조합으로 만들 수 있는 모든 가능한 벡터의 집합입니다.

두 벡터의 조합으로 나올수있는 Span : 면 , 선 , 점(0)

세 벡터의 조합으로 나올수있는 Span : 공간, 면, 선, 점(0)

 

- 선형관계의 벡터 = 두 벡터가 같은 선상에 있을 경우 , 조합이 선으로 제한될때

- 선형관계가 없는 벡터 = 선형관계를 제외한 나머지 , 선형적으로 독립되어 있다 표현

 

• Basis

Span의 역개념 , 공간을 채울수 있는 선형 관계에 있지 않은 벡터들의 모음

 

- Orthogonal Basis : Basis + Orthogonal(수직) : 주어진 공간을 채울 수 있는 서로 수직인 벡터들

- Orthonomal Basis : Orthogonal Basis + Normalized : 길이가 서로 1인

 

• Rank

임의의 행렬 A가 있을 때, 이 행렬의 열들로 생성될 수 있는 벡터 공간의 차원을 의미
행렬 A의 열들 중에서 선형 독립인 열들의 최대의 개수를 Rank
이것은 행에 대해서 나타내어 지는 공간의 차원과도 같다

A라는 행렬의 Column rank는 Column space의 차원을 의미하고 

Row rank는 Row space의 차원을 의미한다. 

결국 행에서 선형 독립인 벡터의 개수와 열에서 선형 독립인 벡터의 개수를 구분해서 정의하겠다는 소리

 

정리하자면 
행렬의 랭크는 행렬이 나타낼 수 있는 벡터 공간에서 기저의 개수를 의미

이 기저는 서로 독립인 행 또는 열의 벡터의 개수에 의해서 결정된다.

열과 행의 랭크는 서로 같은 값을 가지므로,

행렬의 랭크를 구할 때에는 한쪽의 랭크만 계산하면 되고, 서로 선형 독립인 벡터가 몇 개가 되는지만 확인하면 된다. 

 

출처 : blog.naver.com/PostView.nhn?blogId=sw4r&logNo=221416614473&parentCategoryNo=&categoryNo=117&viewDate=&isShowPopularPosts=true&from=search

[기초 선형대수] 행렬에서 Rank (랭크) 란?

 

• Gaussian Elimination

Rank를 확인하는 방법 중 하나

 

• Linear Projections

 

출처 : 코드스테이츠 강의