PCA
Principal Component Analysis
고차원의 데이터를 저차원의 데이터로 환원시키는 기법
데이터의 분산(variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아,
고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법
출처 : ratsgo.github.io/machine%20learning/2017/04/24/PCA/
주성분분석(Principal Component Analysis) · ratsgo's blog
이번 글에서는 차원축소(dimensionality reduction)와 변수추출(feature extraction) 기법으로 널리 쓰이고 있는 주성분분석(Principal Component Analysis)에 대해 살펴보도록 하겠습니다. 이번 글은 고려대 강필성
ratsgo.github.io
RPubs - PCA(Principal component analysis) 분석 예제
rpubs.com
PCA의 개념 및 계산방법을 이해해보자
데이터가 있다




데이터를 시각화하는데 3차원까지는 표현하더라도, 그 이상은 표현하기 어렵다
그래서 PCA 를 통한 시각화를 진행해보자




Gene1 의 평균값을 표시하고
Gene2 의 평균값을 표시한다음
두 평균값이 만나는 점을 기준점으로 삼아 원점으로 이동한다

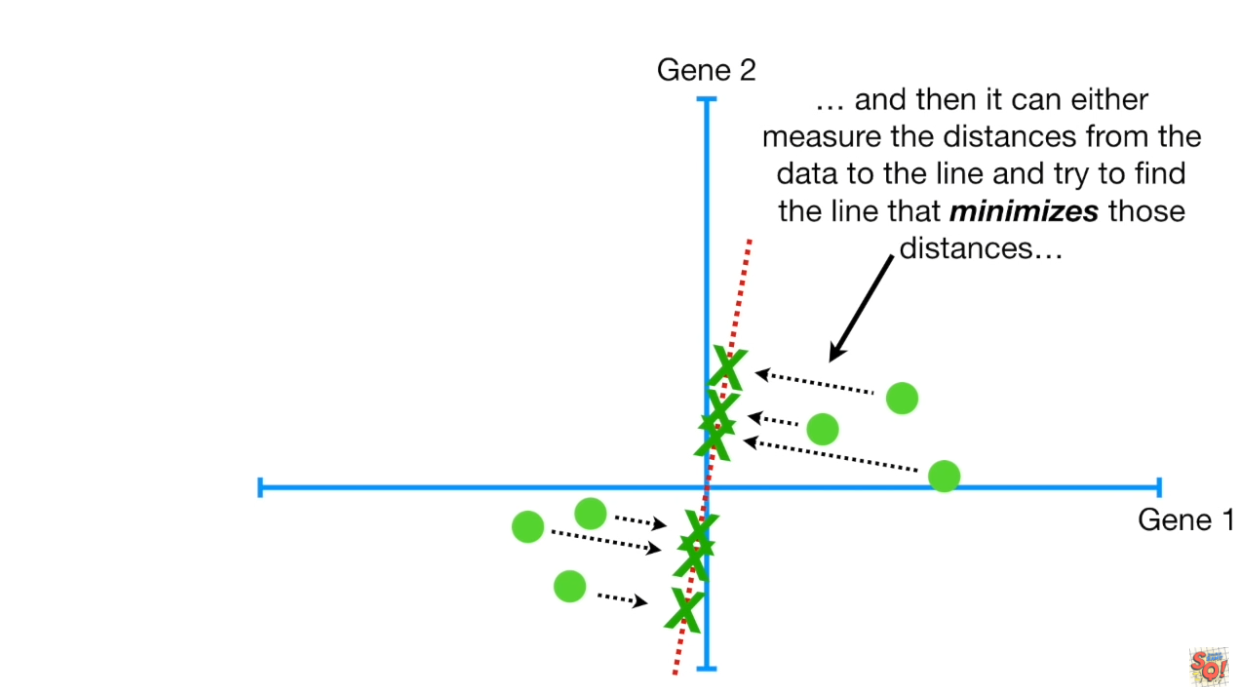

원점을 지나는 임의의 기울기, 직선을 그린 뒤
각 데이터(점) 에서 직선까지의 최소한의 거리
또는 직선에 투영된 점들의 최대한의 거리
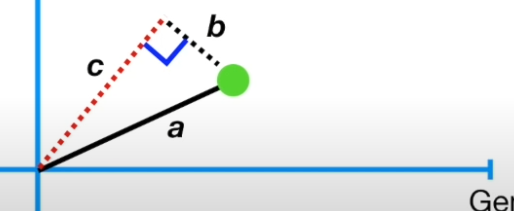
피타고라스 정리를 이용하면
a값은 고정
b의 최소값은 즉 c의 최대값



SS 값이 가장 큰 기울기를 구하는 중

지금 선이 SS 값이 가장 큰 기울기
PC 1
(예시에서 기울기는 0.25라고 가정함)

a**2 = 4**2 + 1**2
a = 4.12

빨간선 (a)라인의 길이 = 4.12
a의 길이를 1로 맞춰주기 위해 (고유벡터로 바꾸기 위해)
모든 길이를 4.12 로 나누면

PC 1 의 고유벡터
'0.97' 과 '0.242' 를 Loading scores for PC1 이라고 함


PC2를 구하는 과정
PC1을 돌려 x축과 평행하게 조절한뒤 그래프 분석



출처 :https://youtu.be/FgakZw6K1QQ
'AI월드 > ⚙️AI BOOTCAMP_Section 1' 카테고리의 다른 글
| 클러스터, scree plot, k-means, ML_Day14(2) (0) | 2021.01.15 |
|---|---|
| HCA(하이어리컬, 클러스터)_Day14 (0) | 2021.01.15 |
| 벡터변환,고유벡터,고유값_Day13(2) (0) | 2021.01.14 |
| eigenvector,eigenvalue,고윳값,고유벡터_Day13 (0) | 2021.01.14 |
| 공분산,상관계수,span,basis,rank_Day12(3) (0) | 2021.01.13 |




댓글