

(왼) 기존 linear regression , 여러 데이터들이 주어져있을때 , least squared
(오) 왼쪽 데이터와 달리 만약 데이터가 그 중 2개만 주어졌다 가정한 뒤 , 두 점을 지나는 곡선 (New Line)


(왼) 빨강선을 training data , 녹색선을 test data라 하고
(오) training model(빨강선)은 빨간점으로부터는 squared residual = 0
하지만 녹색점으로부터는 high variance , 즉 빨강선은 녹색점의 "Over Fit"


(왼,오) 빨강선을 조금 worse 하게 만들어 , variance를 줄이고 결국 model을 fit 하게 만드는 방법

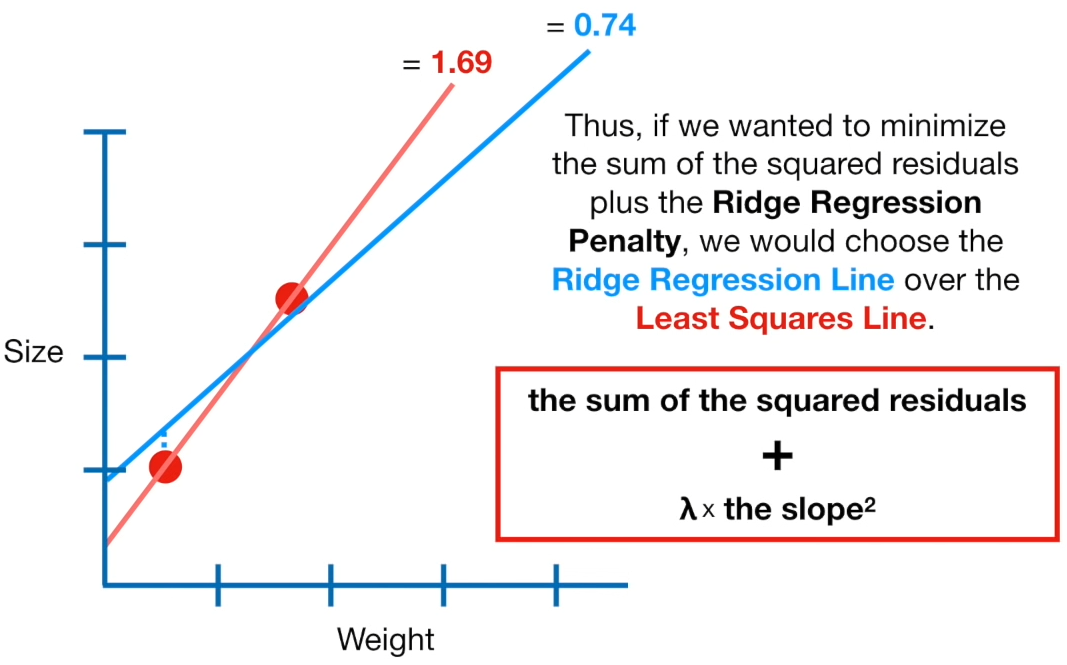
(왼) 빨강선 : the sum of the squared residuals ( 0 , 0 ) + lambda ( 1 ) + the slope**2 ( 1.3**2 ) = 1.69
(오) 파랑선 : the sum of the squared residuals ( 0.3**2 , 0.1**2 ) + lambda ( 1 ) + the slope**2 ( 0.8**2 ) = 0.74
[ 목적 : minimize (squared residuals) + (Ridge regression penalty) ] => 파랑선을 선택해야 한다


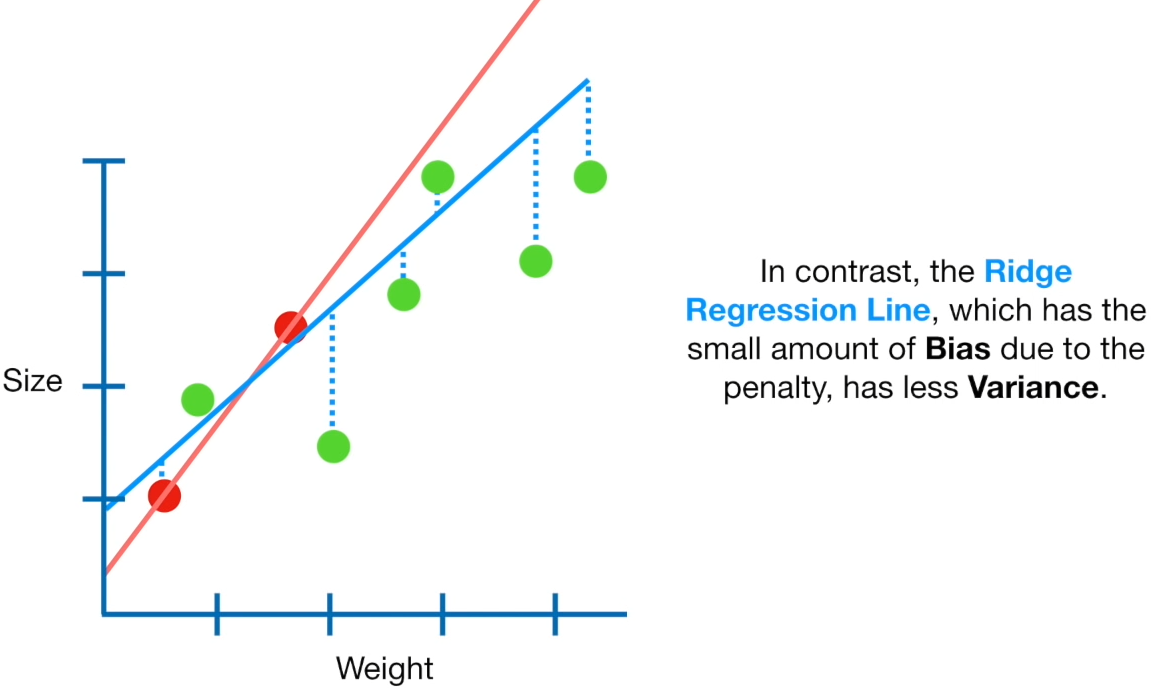
(왼) Bias 없는 빨강선은 큰 variace를 가져온다
(오) 약간은 bias는 vairance를 줄여준다 (약간의 bias를 파악하는 수치 = ridge regression penalty 인듯하다)


(왼) lambda의 값이 커질수록 파랑선의 기울기 내려간다 = weight의 변화에 따라 size의 변화도가 낮아진다
(오) lambda의 값을 대입하면서 가장 낮은 variance가 나오는 model을 찾는다
Ridge Regression 에서 직접 조절 가능한 변수는 lambda 이므로
lambda 값을 조절하면서 최적의 모델을 찾는다

특성이 많아졌을때
"y절편을 제외"하고 모든 변수의 상수제곱이 ridge regression에 포함


size 타겟에 영향을 주는 특성이 1개 (Weight)일때 주어진 데이터가 1개라면 예측 모델 생성 불가능
size 타겟에 영향을 주는 특성이 2개 (Weight , Age )일때 주어진 데이터가 2개라면 예측 모델 생성 불가능




(왼)lambda is determined using Cross validation (비록 traing set 숫자가 적더라도)
(오)Ridge Regression 은 'Cross Validation' & 'Ridge Regression Penalty' 로 찾을수 있다
출처 : youtu.be/Q81RR3yKn30
'AI월드 > ⚙️AI BOOTCAMP_Section 2' 카테고리의 다른 글
| fit_transform과 transform의 차이,싸이킷런 (0) | 2021.02.02 |
|---|---|
| 다중 회귀 분석 vs 다항 회귀 분석_Day23(2) (0) | 2021.02.01 |
| 회귀의 오류지표,MAE,MSE,RMSE,MAPE,MPE_Day22(6) (0) | 2021.01.30 |
| Bias/Variance/편향과분산, 한번더_Day22(5) (0) | 2021.01.30 |
| 과적합(Overfitting)과 과소적합(Underfitting)_Day22(4) (0) | 2021.01.29 |




댓글